Use PyAnsys Math to solve eigenproblems

This example uses a verification manual input file, but you can use your own sparse or dense matrices.

Perform required imports and start PyAnsys

Perform required imports.

import time

from ansys.mapdl.core.examples import vmfiles
import matplotlib.pylab as plt
import numpy as np

import ansys.math.core.math as pymath

# Start PyAnsys Math as a service.
mm = pymath.AnsMath()

Get matrices

Run the input file from Verification Manual 153 and then get the stiff (k) and mass (m) matrices from the FULL file.

out = mm._mapdl.input(vmfiles["vm153"])
fullfile = mm._mapdl.jobname + ".full"
k = mm.stiff(fname=fullfile)
m = mm.mass(fname=fullfile)

Display size of the matrices

Display size of the k and m matrices.

print(m.shape)
print(k.shape)

(63, 63)
(63, 63)

Allocate an array to store eigenshapes

Allocate an array to store the eigenshapes, where nev` is the number of eigenvalues requested,

nev = 10
a = mm.mat(k.nrow, nev)
a

AnsMath dense matrix (63, 10

Perform modal analysis

Perform the modal analysis.

The algorithm is automatically chosen with respect to the properties of the matrices (such as scalar, storage, or symmetry).

print("Calling PyAnsys Math to solve the eigenproblem...")

t1 = time.time()
ev = mm.eigs(nev, k, m, phi=a)
print(f"Elapsed time to solve this problem: {time.time() - t1}")

Calling PyAnsys Math to solve the eigenproblem...
Elapsed time to solve this problem: 0.030966997146606445

Print eigenfrequencies

Print the vector of eigenfrequencies.

print(ev)

VFZGHZ :
 Size : 10
  2.113e+02   4.865e+02   7.701e+02   1.065e+03   1.375e+03      <       5
  1.517e+03   1.517e+03   1.709e+03   1.747e+03   1.747e+03      <       10

Verify the accuracy of eigenresults

Check the residual error for the first eigenresult: \(R_1=||(K-\lambda_1.M).\phi_1||_2\)

First, compute \(\lambda_1 = \omega_1^2 = (2.\pi.f_1)^2\)

# Eigenfrequency (Hz)
i = 0
f = ev[0]
omega = 2 * np.pi * f
lam = omega * omega

Then get the first eigenshape \(\phi_1\) and compute both \(K.\phi_1\) and \(M.\phi_1\).

# shape
phi = a[0]

# APDL command: *MULT,K,,Phi,,KPhi
kphi = k.dot(phi)

# APDL command: *MULT,M,,Phi,,MPhi
mphi = m.dot(phi)

Next, compute the \(||K.\phi_1||_2\) quantity and normalize the residual value.

# APDL command: *MULT,K,,Phi,,KPhi
kphi = k.dot(phi)


# APDL command: *NRM,KPhi,NRM2,KPhiNrm
kphinrm = kphi.norm()

Add these two vectors, using the \(\lambda_1\) scalar factor, and compute the normalized residual value: \(\frac{R_1}{||K.\phi_1||_2}\)

# APDL command: *AXPY,-lambda,,MPhi,1,,KPhi
mphi *= lam
kphi -= mphi

# Compute residual
res = kphi.norm() / kphinrm
print(res)

1.9136679485631705e-10

Compute this residual for all eigenmodes

def get_res(i):
    """Compute the residual for a given eigenmode."""
    # Eigenfrequency (Hz)
    f = ev[i]

    # omega = 2.pi.Frequency
    omega = 2 * np.pi * f

    # lambda = omega^2
    lam = omega * omega

    # i-th eigenshape
    phi = a[i]

    # K.Phi
    kphi = k.dot(phi)

    # M.Phi
    mphi = m.dot(phi)

    # Normalize scalar value
    kphinrm = kphi.norm()

    # (K-\lambda.M).Phi
    mphi *= lam
    kphi -= mphi

    # Return the residual
    return kphi.norm() / kphinrm


pymath_acc = np.zeros(nev)

for i in range(nev):
    f = ev[i]
    pymath_acc[i] = get_res(i)
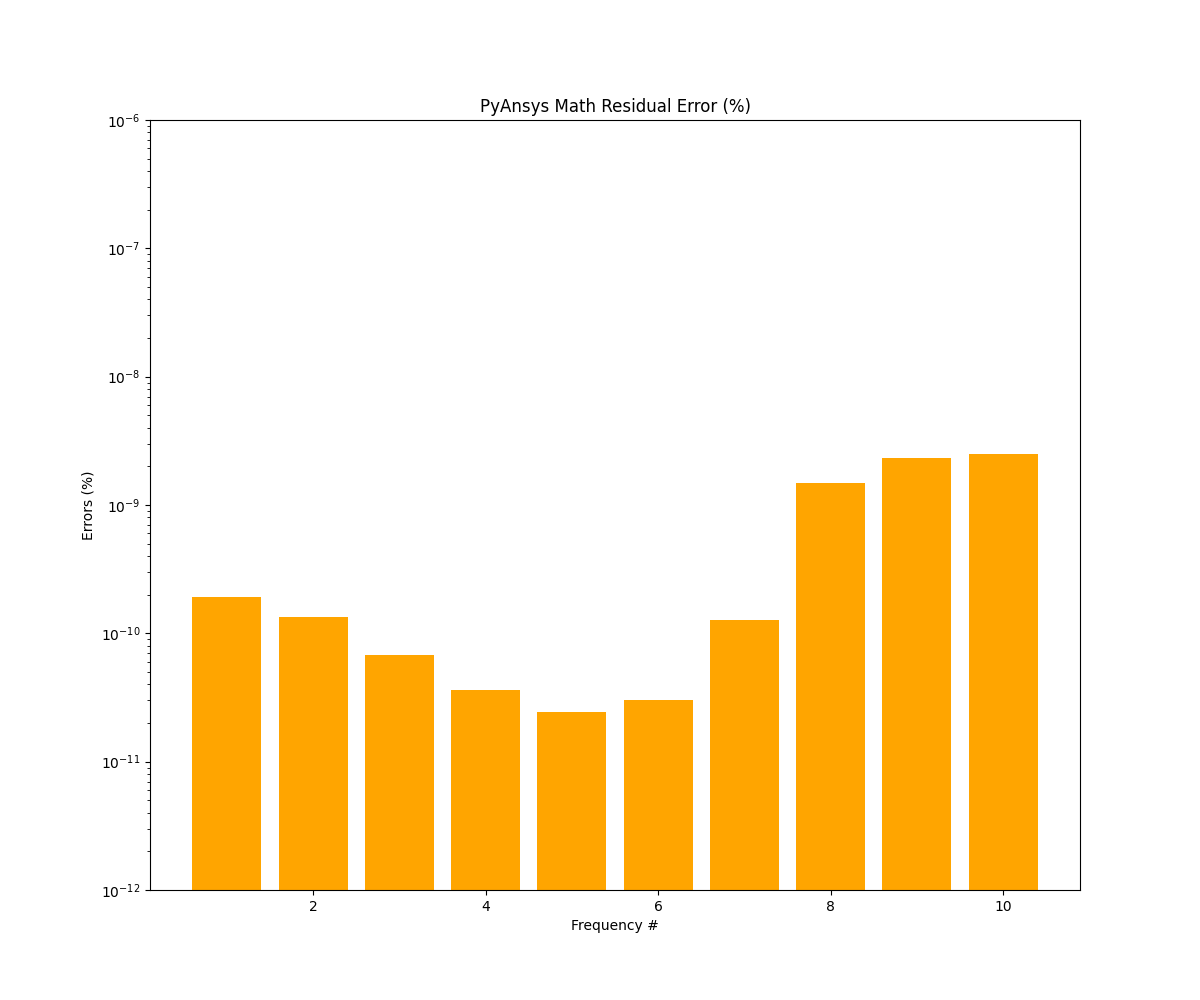
    print(f"[{i}] : Freq = {f}\t - Residual = {pymath_acc[i]}")

[0] : Freq = 211.2534447881588   - Residual = 1.9136679485631705e-10
[1] : Freq = 486.50419022721263  - Residual = 1.3403406950622093e-10
[2] : Freq = 770.104536570519    - Residual = 6.739462952718192e-11
[3] : Freq = 1064.5432295081987  - Residual = 3.631667679775435e-11
[4] : Freq = 1374.535393913082   - Residual = 2.426773924787909e-11
[5] : Freq = 1516.8545419017319  - Residual = 3.024157834515717e-11
[6] : Freq = 1516.8545419017403  - Residual = 1.2726936409880203e-10
[7] : Freq = 1708.9655656955329  - Residual = 1.4727869229348076e-09
[8] : Freq = 1747.1764513661403  - Residual = 2.311798816791578e-09
[9] : Freq = 1747.176451366141   - Residual = 2.5094281080563296e-09

Plot accuracy of eigenresults

Plot tahe accuracy of the eigenresults.

fig = plt.figure(figsize=(12, 10))
ax = plt.axes()
x = np.linspace(1, nev, nev)
plt.title("PyAnsys Math Residual Error (%)")
plt.yscale("log")
plt.ylim([10e-13, 10e-7])
plt.xlabel("Frequency #")
plt.ylabel("Errors (%)")
ax.bar(x, pymath_acc, label="PyAnsys Math Results", color="orange")
plt.show()

Stop PyAnsys Math

Stop PyAnsys Math.

mm._mapdl.exit()

/opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/ansys/mapdl/core/launcher.py:811: UserWarning: The environment variable 'PYMAPDL_START_INSTANCE' is set, hence the argument 'start_instance' is overwritten.
  warnings.warn(